Computing Certain Properties of Additive and Multiplicative Groups of Integers Modulo n Utilizing MATLAB

Introduction

Bjarne Stroustrup pioneered the development of an extension to the C programming language, known as C++, during the early 1980s [4]. In the late 1980s, Microsoft Corp.TM introduced its C++ compiler, bundled with a collection of library functions known as the Microsoft Foundation Classes (MFC) [6]. The MFC compiler proved to be a robust tool, empowering programmers to effortlessly design buttons, menus, dialog boxes, as well as incorporate text and graphics to visualize problem-solving. It offered a streamlined approach to making corrections and modifications. This enhanced user-friendliness and visual appeal of the program.

MATLAB was primarily developed by Cleve Moler, a renowned computer scientist and mathematician [3]. Moler’s vision for MATLAB was to create a user-friendly environment for matrix computations and numerical analysis. His work on MATLAB has had a profound impact on scientific and engineering fields, as MATLAB has become an indispensable tool for researchers, engineers, and students worldwide, facilitating complex computations and data analysis. Cleve Moler’s contribution to computational mathematics and software development is highly regarded in the scientific community.

MATLAB, as highlighted in [7], stands as a high- performance language tailored for technical computing tasks. Its distinguishing feature lies in its seamless integration of computation, visualization, and a comprehensive programming environment. Furthermore, MATLAB presents itself as a contemporary programming language environment, replete with advanced data structures, in-built editing and debugging utilities, and robust support for object- oriented programming. These characteristics collectively position MATLAB as an invaluable resource for both educational and research purposes. In comparison to traditional programming languages such as C and FORTRAN, MATLAB boasts numerous advantages when it comes to addressing technical challenges. Notably, MATLAB operates as an interactive system where arrays serve as its fundamental data element, eliminating the need for explicit dimensioning. This software package, commercially accessible since 1984, has achieved the status of a standard tool across numerous universities and industries worldwide.

MATLAB impressively incorporates potent built-in routines that facilitate an extensive array of computations. Additionally, it offers user-friendly graphics commands that promptly provide visual representations of results. Specific applications are conveniently bundled in packages known as toolboxes, each tailored to distinct domains like signal processing, symbolic computation, control theory, simulation, optimization, and various other fields within applied science and engineering.

This research centers on the analysis of various properties within Group Theory, encompassing the determination of group order, individual element orders and inverses, identification of cyclic subgroups and compilation of generator lists. In a prior study, Mohd Ali and Sarmin [1] developed a C++ program interface to display the properties of two finite abelian groups: the group of integers under addition modulo n, denoted as \(Z_n\) , and the group of integers under multiplication modulo n, denoted as \((Zn)^*\), where n represents a positive integer. However, the previous program had limitations, restricting input values of n to a maximum of 120 and displaying all group properties in a single interface. Later on, Mohd Ali, Noor Azhuan, Sarmin, and Johar [2] endeavored to simulate these group properties for extended integer values, specifically \(n\) ≦ 200, while allowing users to select their preferred property for display.

Inspired by the work of Mohd Ali, Noor Azhuan, Sarmin, and Johar [2], who explored the computation of properties of additive and multiplicative groups of integers modulo n using C++ programming, this research report delves into the same domain but with a novel approach. In this study, we leverage the power of MATLAB as our primary computational tool, offering enhanced capabilities and versatility. Notably, our research extends the boundaries by accommodating values of n up to 300, addressing a limitation present in the previous work. This novel software additionally empowers users to select their preferred property for display, offering a tailored and customizable experience. Through this endeavor, we aim to provide a comprehensive and refined analysis of these groups, shedding new light on their properties and applications.

2. The groups \(Z_{n}\) and \(Z_{n}\)^*

In this section, we provide relevant definitions and properties of groups. Additionally, we offer an explanation of how to derive certain properties of \(Z_n\) and \((Z_n)^*\).

Definition 2.1.

Order of a Group [5]

The number of elements of a group is called the group’s order. The notation |\(G\)| is used to denote the order of \(G\).

Definition 2.2.

Order of an Element [5]

The order of an element \(g\) in a group \(G\) is the smallest positive integer n such that gⁿ = e (in additive notation, it would be ng = 0). The order of an element g is denoted by |\(g\)|.

Definition 2.3.

Cyclic Subgroup [5]

Let \(G\) be a group and a ∈ \(G\). Then ⟨a⟩ = {an | n ∈ \(Z\)} is called a cyclic subgroup of \(G\) generated by a.

Definition 2.4.

The Group \(Z_n\) [2]

The set \(Z_n\) = {0, 1, 2, . . . , \(n\)−1} for \(n\) ≤ 1 is a group under addition modulo n. For any \(i\) in \(Z_n\) , the inverse of \(i\) is \(n\)−\(i\). This group is commonly known as the group of integers modulo \(n\).

Theorem 2.1.

[5] In a finite group G, the order of each element a in \(G\) divides the order of \(G\). In symbols, we write |\(a\)|||\(G\)|, for all \(a\) ∈ \(G\).

Next we give an example of the group \(G_{15}\), the group of integers under addition modulo \(15\), with some of its properties.

Example 2.1.

The elements of \(G_{15}\) are {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}. Hence, its order is 15. The computations of the order of the elements are as follows: |0| = 1 since the order of the identity element is always 1. |1| = |2| = |4| = |7| = |8| = |11| = |13| = |14| = 15 since 15 × 1 ≡ 0, 15 × 12 ≡ 0, 15 × 4 ≡ 0 |10| = |5| = 3 and |3| = |6| = |9| = |12| = 5.

Now, to get the inverse of each element, we use the formula \(n\) − \(i\), where \(i\) is the element in \(Z_{15}\). Therefore, 0−1 = 0 (the inverse of the identity element is itself ), 1⁻¹ = 14, 2⁻¹ = 13, 3⁻¹ = 12, 4⁻¹ = 11, 5⁻¹ = 10, 6⁻¹ = 9, 7⁻¹ = 8, 8⁻¹ = 7, 9⁻¹ = 6, 10⁻¹ = 5, 11⁻¹ = 4, 12⁻¹ = 3, 13⁻¹ = 2, and 14⁻¹ = 1. The elements 1, 2, 4, 7, 8, 11, 13, and 14 are generators of this group, since their order is the same as the order of \(Z_{15}\). The cyclic subgroups of \(Z_{15}\) are obtained by generating each element of \(Z_{15}\). The following subgroups are the cyclic subgroups of \(Z_{15}\):

= {0}, == {0, 5, 10} ======== Z₁₅ ==== {0, 3, 6, 9, 12}

Definition 2.5.

The Group \(Z^*_n\). [5]

\(Z^*_n\) is defined to be the set of all positive integers less than \(n\) and relatively prime to \(n\) for each \(n\) > 1. Then \(Z^*_n\) is a group under multiplication modulo \(n\).

Now we give an example of the group \(Z^*_n\), the group of integers under multiplication modulo 15, with some of its properties.

Example 2.2.

The elements of \(Z^*_n\) are {1, 2, 4, 7, 8, 11, 13, 14}. So its order is 8.

The orders of the elements are as follows: |1| = 1 since the order of the identity element is always 1. |2| = 4 since 24 ≡ 16 ≡ 1 (mod 15), |4| = 2 since 42 ≡ 16 ≡ 1 (mod 15), |7| = 4 since 74 ≡ 2401 ≡ 1 (mod 15), |8| = 2 since 82 ≡ 64 ≡ 1 (mod 15), |11| = 4 since 114 ≡ 14641 ≡ 1 (mod 15), |13| = 4 since 134 ≡ 28561 ≡ 1 (mod 15), |14| = 2 since 142 ≡ 196 ≡ 1 (mod 15). The inverses of each element are: 1⁻¹ = 1, 2⁻¹ = 8, 4⁻¹ = 4, 7⁻¹ = 13, 8⁻¹ = 8, 11⁻¹ = 11, 13⁻¹ = 7, and 14⁻¹ = 14. The inverse of the identity element is itself. Moreover, this group has no generator and the cyclic subgroups of \(Z^*_n\) are also obtained by generating each element of \(Z^*_n\). The following subgroups are the cyclic subgroups of \(Z^*_n\)

: = {1}, = = {1, 2, 4, 8}, = {1, 4}, = = {1, 7, 4, 13}, = {1, 11} and ={1, 14}.

3. The Program code for the group \(Z_n\)

Within this section, we provide programming code snippets along with their corresponding output displays. The purpose of the program is to comprehensively analyze various aspects of the group \(Z_n\). Specifically, it is designed to ascertain the complete set of group elements, the group’s order, an element’s inverse, an element’s order, group generators, and cyclic subgroups.

To utilize the program effectively, one must input the value of interest, prompting the program to present a menu of available properties. Users can then select their desired property, and the program will promptly generate and display the corresponding output.

The following provided code is instrumental in determining each property within the context of the group \(Z_n\). Next, we will explore an example with \(n\) ranging from 0 to 300, for the group \(Z_n\).

3.1 The Computation n the Group (Z₂₀₉)

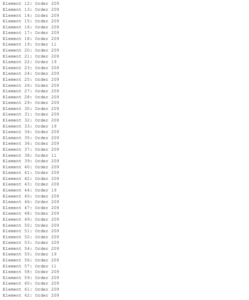
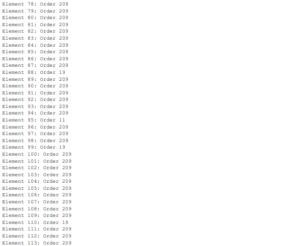
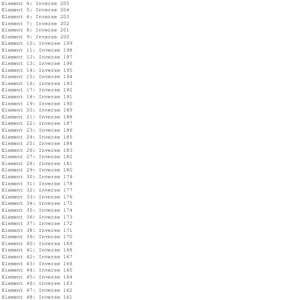
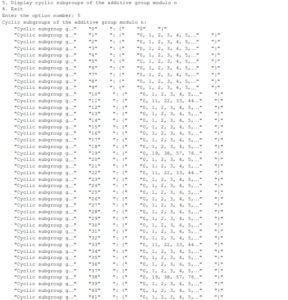
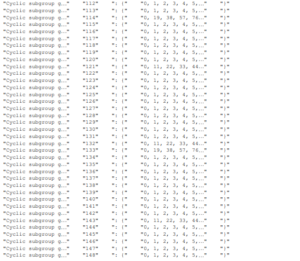
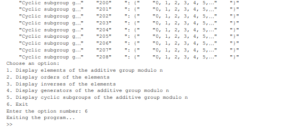
4. The program code for the group \(Z^*_n\)

Within this section, we provide programming code snippets along with their corresponding output displays. The purpose of the program is to comprehensively analyze various aspects of the group \(Z^*_n\). Specifically, it is designed to ascertain the complete set of group elements, the group’s order, an element’s inverse, an element’s order, group generators, and cyclic subgroups.

To utilize the program effectively, one must input the value of interest, prompting the program to present a menu of available properties. Users can then select their desired property, and the program will promptly generate and display the corresponding output.

The following provided code is instrumental in determining each property within the context of the group \(Z^*_n\). Next, we will explore an example with \(n\) ranging from 0 to 300, for the group \(Z^*_n\).

4.1 The Computations in the group \(Z^*_210\)

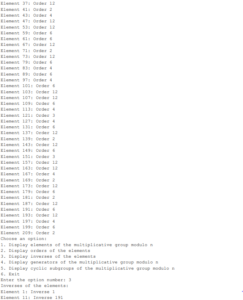
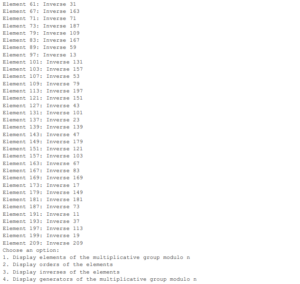
5. Summary

This software has been developed with the explicit purpose of calculating various properties of a group. These properties encompass the identification of all elements within the group, determination of the group’s order, computation of the inverses and orders of individual elements, identification of group generators, and the exploration of cyclic subgroups within the groups \(Z_n\) and \(Z^*_n\).

To utilize the program, you simply input your desired value for ’n’ and then select one of the available options. Subsequently, the program will generate and display the relevant properties based on your selection. It is our aspiration that this program will serve as an initial step towards the creation of more advanced and sophisticated software tools for similar purposes.

Acknowledgements

The authors would like to express their sincere gratitude to GIFT University, Gujranwala, Pakistan, for their support and resources that facilitated this research. This work was made possible through the academic and research environment provided by the School of Engineering and Applied Sciences, Department of Computer Sciences at GIFT University.

References

1. Mohd Ali, N. M., & Sarmin, N. H. (2010). On some problems in group theory of probabilistic nature. Menemui Matematik (Discovering Mathematics), 32(2), 35-41.
2. Mohd Ali, N. M., Noor Azhuan, N. A., Sarmin, N. H. & Johar, F. (2017). The Computation of Some Properties of Additive and Multiplicative Groups of Integers Modulo n Using C++ Programming. Sains Humanika, 9(1-2), 57-63.
3. Attaway, S. (2013). MATLAB: A Practical Introduction to Programming and Problem Solving. Elsevier Inc.
4. Deitel, H. M., & Deitel, P. J. (2013). C++ How to Program (9th ed.). Prentice Hall.
5. Fraleigh, J. B. (2003). A First Course in Abstract Algebra (7th ed.). Reading, Massachusetts.
6. Garret, P. B. (2008). Abstract Algebra (6th ed.). Chapman and Hall/CRC.
7. The Mathworks Inc. (2005). MATLAB 7.0 (R14SP2). The MathWorks Inc.